I defended my master's thesis on Diffusion-Based Evolutionary Algorithms

Context

On May 13th, 2025, I defended my master’s thesis on Denoising Diffusion-Based Evolutionary Algorithms and I graduated from the Technical University of Vienna with a Master’s degree in Data Science 🎓.

Working on this thesis was a great experience, starting with all the learnings I take:

• I learned a lot about diffusion models, their implementation and their training.
• I dived deep into the original DIFUSCO paper and its tricks and deatils.
• On the technical side, I learned a ton of PyTorch and PyTorch Geometric, and I looked into nice libraries like EvoTorch.

I had a great supervisor, Günther Raidl, who provided me with excellent guidance and support. He suggested writing a paper about our DDEA framework, which will put a perfect end to my master’s thesis.

In the following, I will give a brief overview of our work in the form of a technical report.

Update (18. Oct 2025): the paper was accepted at LOD 2025!

• arXiv Link

Abstract

I present a novel Denoising Diffusion-based Evolutionary Algorithm (DDEA) framework that synergistically integrates denoising diffusion models with evolutionary algorithms for combinatorial optimization. DDEA leverages pre-trained diffusion models for both high-quality population initialization and a novel diffusion-based recombination operator trained via imitation learning from an optimal demonstrator.

Evaluating DDEA on the Maximum Independent Set Problem on Erdős-Rényi graphs, I demonstrate significant improvements over DIFUSCO, a leading diffusion-based solver. DDEA consistently outperforms DIFUSCO given the same time budget and surpasses Gurobi on larger graphs, with solution sizes being 3.9% and 7.5% larger on the ER-300-400 and ER-700-800 datasets, respectively. In out-of-distribution experiments, DDEA provides solutions of 11.6% higher quality than DIFUSCO under the same time limit.

This work highlights the potential of hybridizing diffusion models and evolutionary algorithms, offering a promising direction for developing powerful machine learning solvers for complex combinatorial optimization problems.

Introduction

Combinatorial optimization problems involve finding optimal solutions from discrete but often enormous sets of candidates. Many of these problems are NP-hard and challenging to solve in practice, especially for large instances. Traditional approaches rely on methods like Integer Linear Programming (ILP) or carefully designed metaheuristics, which often require substantial domain expertise and may struggle with scalability.

Recent advances in deep learning have introduced new methods for tackling combinatorial optimization, with denoising diffusion models (DDMs) emerging as particularly promising. Frameworks like DIFUSCO demonstrate that DDMs can generate diverse, high-quality candidate solutions efficiently by leveraging their ability to learn complex probability distributions over solution spaces. However, these diffusion-based methods face significant challenges: they often require problem-specific post-processing heuristics to ensure feasibility and may struggle to generalize effectively to different problem sizes or variants.

This highlights a critical gap: while DDMs excel at generating potentially diverse solutions, they frequently lack the robust, structured exploration mechanisms inherent in classical metaheuristics like evolutionary algorithms (EAs). Conversely, EAs provide a general framework for robust search but can struggle without effective methods to initialize populations with high-quality, diverse individuals or to generate promising offspring through recombination.

To bridge this gap, I propose the Denoising Diffusion-based Evolutionary Algorithm (DDEA), a novel hybrid framework that integrates pre-trained DDMs into core operators of an EA. DDEA uses DDMs for both high-quality population initialization and a novel diffusion-based recombination operator trained via imitation learning from an optimal demonstrator. This synergy aims to combine the efficient generation of diverse, high-quality solutions from DDMs with the problem-agnostic exploratory capabilities of EAs.

Method

I demonstrate DDEA on the Maximum Independent Set Problem (MISP), a classic combinatorial optimization problem. Given an undirected graph $G=(V,E)$, the goal is to find the largest subset of vertices $S \subseteq V$ such that no two vertices in $S$ are adjacent. This problem is NP-hard and serves as an excellent testbed for evaluating optimization algorithms.

DDEA Framework Overview

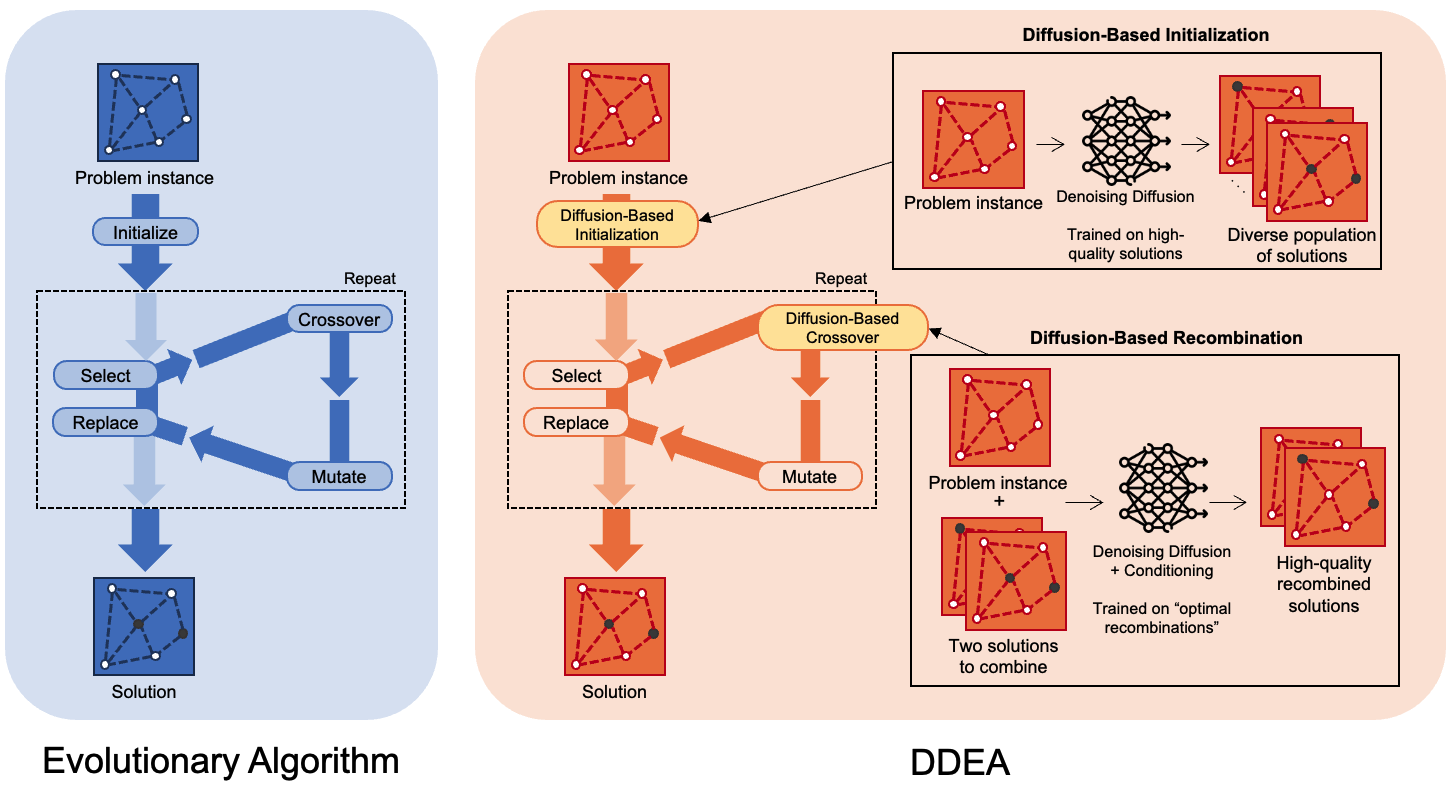
The core idea of DDEA is to augment specific components of a standard evolutionary algorithm—namely initialization and recombination—with operations guided by a pre-trained diffusion model. DDEA retains the standard EA loop: parent selection, recombination, mutation, and replacement with elitism.

Solution Representation and Decoding

DDEA encodes candidate solutions as binary incidence vectors of size $n=\lvert V \rvert$, where each element $x_i$ represents whether node $i \in V$ is included in the independent set. A key component is the decoding process that transforms probability vectors from the diffusion model into feasible solutions.

Given a probability vector $\mathbf{p} \in [0,1]^n$ representing the likelihood of each node being in the independent set, the decoding algorithm:

1. Sorts all nodes in descending order of their probability scores
2. Processes nodes in this order, including each node if it hasn’t been marked as ineligible
3. Marks all neighbors of included nodes as ineligible to maintain feasibility

This greedy construction ensures that high-probability nodes are prioritized while maintaining feasibility at each step.

Diffusion-Based Initialization

To generate a high-quality and diverse initial population, DDEA leverages a pre-trained DIFUSCO model. DIFUSCO exhibits multi-modal properties, enabling it to sample diverse solutions from the underlying distribution when starting from different noise. This makes it well-suited for initializing an EA population.

The initialization process involves two steps:

1. Sample node probability vectors $\mathbf{p}_j \in [0,1]^n$ from the pre-trained DIFUSCO model in parallel
2. Decode all probability vectors into feasible candidate solutions using the greedy decoding heuristic

Diffusion-Based Recombination

Traditional crossover operators are often generic and may not effectively preserve beneficial structural information specific to the problem domain. The diffusion-based recombination operator aims to be more intelligent and problem-aware by using a conditional diffusion model trained to generate high-quality offspring from parent solutions.

Expert Demonstrator for Training Data Generation

To train the recombination model, I generate high-quality training data using an expert demonstrator—an Integer Linear Program (ILP) that finds the best solution in a restricted search space around two parent solutions. The ILP maximizes the offspring independent set size while constraining the combined Hamming distance from both parents, allowing controlled exploration around the parental solutions.

Training via Imitation Learning

The diffusion recombination model is trained using imitation learning on the expert demonstrations. During training, the model learns to predict how to reduce noise to ultimately obtain the expert offspring, conditioned on the parent solutions and the graph structure. This approach allows DDEA to generate new solutions that are not random combinations of parents but are guided by the learned distribution of high-quality solutions.

Experiments & Results

I evaluate DDEA on Erdős-Rényi (ER) random graphs of varying sizes, focusing on three key aspects: component evaluation, ablation studies, and benchmarking against other methods.

Experimental Setup

Datasets: I use ER graphs with edge probability 0.15 and three different node ranges: [50, 100], [300, 400], and [700, 800]. For each range, 40,000 graphs were created for training, with 128 held out for testing. Ground truth labels are obtained using KaMIS with a 60-second time limit.

Implementation: DDEA uses PyTorch Geometric and EvoTorch, with diffusion models based on DIFUSCO. The recombination operator is trained using Gurobi 12.0 for the ILP-based expert demonstrator with a 15-second time limit per call.

Diffusion Recombination Evaluation

I first evaluate the diffusion recombination operator in isolation by comparing it against baseline methods using parents of varying quality. The results show that the diffusion recombination effectively approximates the expert operator, outperforming both DIFUSCO and traditional crossover methods. Performance degrades gracefully with decreasing parent quality, demonstrating cost monotonicity and validating the design.

Ablation Studies

Ablation studies confirm that both diffusion-based initialization and recombination are crucial components. The full DDEA achieves performance comparable to expert optimized recombination while drastically reducing runtime per generation (e.g., 5s vs. 88s on ER-300-400). The learned diffusion recombination effectively approximates the expensive ILP solving, enabling near-expert performance in practical runtimes.

Key findings from the ablation studies:

• Diffusion recombination is particularly impactful: Comparing full DDEA to variants without diffusion recombination shows substantial benefits (e.g., 2.81% vs. 5.75% gap on ER-700-800)
• Diffusion initialization provides consistent benefits: While recombination is more critical, diffusion initialization consistently improves performance across all datasets
• The framework is robust: Even with greedy initialization, diffusion recombination performs well compared to naive baselines

Benchmarking Against Other Methods

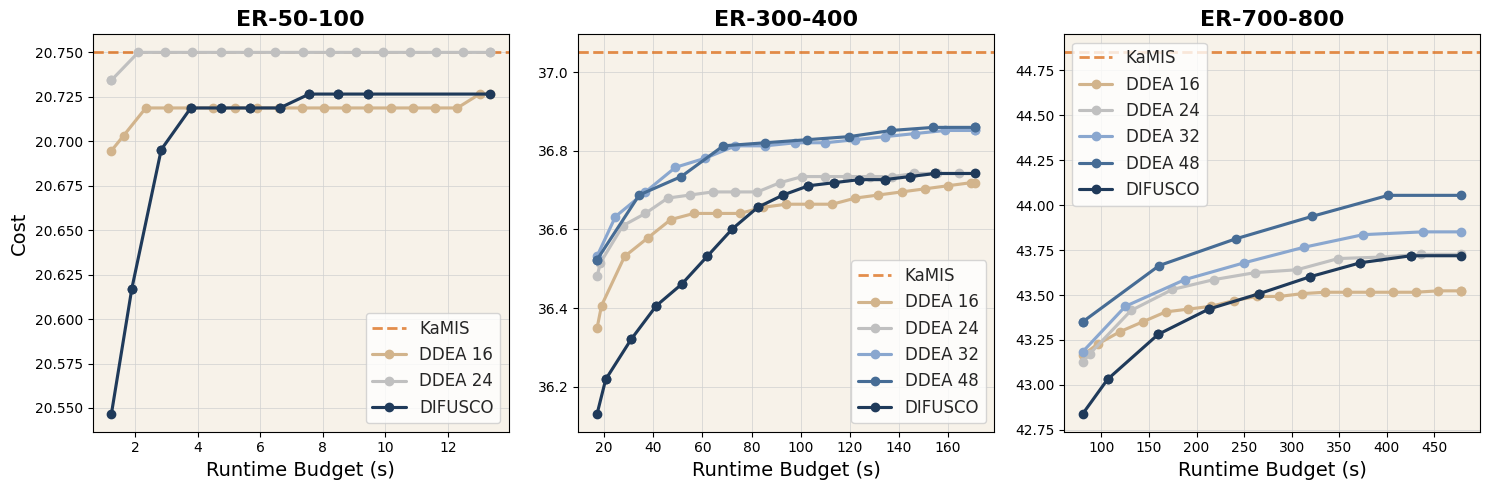
The results demonstrate DDEA’s superiority over existing methods:

Comparison with DIFUSCO: DDEA consistently outperforms DIFUSCO given the same time budget across all datasets. On ER-50-100, DDEA achieves optimal solutions in just two generations. On larger graphs (ER-300-400 and ER-700-800), DDEA maintains superior performance throughout the considered time budgets.

Comparison with Gurobi: DDEA outperforms Gurobi on larger graphs, achieving solution sizes that are 3.9% and 7.5% larger on ER-300-400 and ER-700-800 datasets, respectively. On ER-50-100, DDEA matches Gurobi’s performance, solving the dataset to optimality.

Out-of-Distribution Generalization: On the ER-1300-1400 dataset (larger than training instances), DDEA achieves notably higher solution quality than DIFUSCO with similar runtime. DDEA’s primal integral (2.27) significantly exceeds DIFUSCO’s (1.21), demonstrating effective use of evolutionary search to find solutions beyond the training distribution.

Key Performance Metrics

• Runtime Efficiency: DDEA achieves near-expert performance while reducing recombination time from 88s to 5s per generation
• Solution Quality: Consistently outperforms DIFUSCO and Gurobi on larger graphs
• Generalization: 11.6% better than DIFUSCO on out-of-distribution tasks
• Scalability: Maintains performance across different graph sizes and problem instances

Conclusion

I presented DDEA, a novel framework that successfully integrates denoising diffusion models with evolutionary algorithms for combinatorial optimization. By leveraging diffusion models for both population initialization and recombination, DDEA combines the generative strengths of DDMs with the robust search capabilities of EAs.

Key Contributions:

1. Novel Hybrid Framework: DDEA demonstrates how to effectively integrate pre-trained diffusion models into core EA operators, going beyond using DDMs merely as solution generators
2. Diffusion-Based Recombination: A novel recombination operator trained via imitation learning from an optimal demonstrator, enabling intelligent offspring generation
3. Strong Empirical Results: DDEA consistently outperforms both DIFUSCO and Gurobi on the Maximum Independent Set Problem, with particularly strong performance on larger graphs
4. Robust Generalization: Superior out-of-distribution performance demonstrates the framework’s ability to adapt beyond training distributions

Impact and Future Directions:

DDEA highlights the potential of hybridizing diffusion models and evolutionary algorithms, offering a promising direction for developing effective combinatorial optimization solvers. The framework is problem-agnostic and can be applied to other CO problems with minimal adaptations.

Future work could explore optimizing diffusion inference parallelization for substantial runtime improvements, investigating cheaper methods for generating recombination training data, and applying DDEA to other combinatorial optimization problems. The success of this hybrid approach suggests that combining the generative strengths of modern ML models with the structured search of classical metaheuristics is a fruitful research direction.

This work bridges the gap between pure learning-based methods and specialized classical algorithms, demonstrating that the best solutions often come from thoughtfully combining different paradigms rather than choosing between them.