A ViT-based Siamese Network for Visual Reasoning in the KiVA-ICCV Challenge (2nd-place solution!)

Context

I participated in the KiVA Challenge, part of the 3rd Perception Test Challenge at ICCV 2025. The Perception Test Challenge presents a series of challenges that test the ability of AI systems to percept visual information. The KiVA challenge specifically tests the ability of AI systems to reason about visual analogies.

I decided to participate as an opportunity to strengthen my computer vision skills, and was totally worth it: I had a great time working on the challenge, and I learned a lot. My solution placed second in the leaderboard, and was one of the four awarded solutions. In the following, I present the details of my solution in the form of a technical report.

Full report (PDF): KiVA Challenge Report

Code: github.com/jsalvasoler/kiva-iccv

Update (24. Oct 2025): I was awarded the 2nd-place solution!

Abstract

We present a novel Vision Transformer (ViT)-based Siamese network for visual analogical reasoning developed for the Kid-inspired Visual Analogies (KiVA) Challenge. This architecture achieves 95.9% accuracy on the benchmark, demonstrating strong performance across all difficulty levels and establishing the effectiveness of the architecture for visual reasoning tasks.

Introduction

Visual analogical reasoning, the ability to infer and apply abstract rules from visual examples, is a hallmark of human intelligence and a critical component of flexible, general-purpose problem-solving. The KiVA benchmark provides a framework for evaluating this capability in AI systems, grounding the task in developmental psychology by using simple transformations of everyday objects that are solvable even by young children.

The challenge frames this task in the classic A:B :: C:? format, where a model must identify the transformation that turns A into B and apply it to C to find the correct outcome among several choices. Here’s an example of a KiVA task:

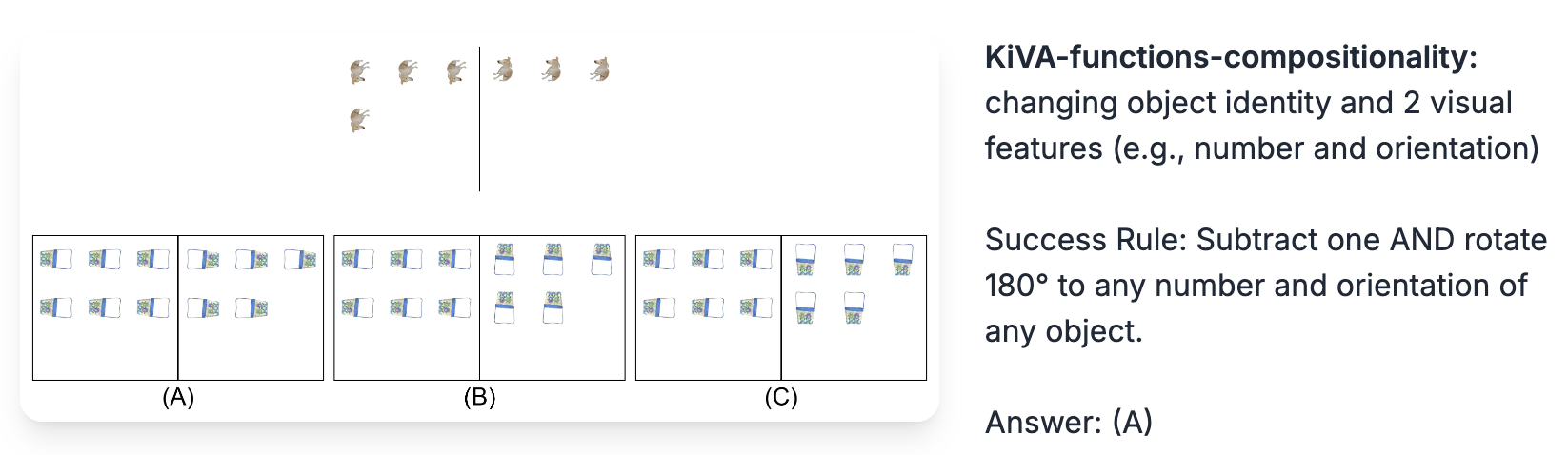
Difficulty Levels

The KiVA benchmark comprises three difficulty levels:

1. KiVA (easy): Only the object identity changes between the example and test transformations
2. KiVA-functions (moderate): Both the object identity and one visual feature (such as orientation, size, or number) change
3. KiVA-functions-compositionality (difficult): The object identity and two visual features (e.g., orientation, size, or number) change between the example and test

This progression allows for a systematic evaluation of analogical reasoning as the complexity of the required transformation increases.

Method

Our approach employs a Siamese Network designed specifically for visual analogical reasoning. Given an example transformation pair (\(A\), \(B\)) and a test scenario \(C\) with multiple candidate choices (\(D_1, \dots, D_n\)), the model must identify which choice correctly completes the analogy.

Architecture Overview

The model operates as follows:

1. The example transformation (\(A\), \(B\)) is encoded using a transformation encoder to produce a transformation vector \(\mathbf{t}_{\mathrm{AB}}\)
2. Each candidate transformation \((C, D_1), \ldots, (C, D_n)\) is similarly encoded to produce choice vectors \(\mathbf{t}_{\mathrm{CD}_i}\)
3. The goal is to identify the choice \(i\) where \(\mathbf{t}_{\mathrm{CD}_i}\) is most similar to \(\mathbf{t}_{\mathrm{AB}}\), typically measured using cosine similarity

An important detail of our approach is that we assume that the eight images of the KiVA task can be extracted from the “stitched” image. It is a fair assumption, as the complexity of the task is the same when the images are given separately. Moreover, it would be simple to train a model to extract the images from the stitched image, if necessary. In our KiVA task, with \(n=3\), we refer to these images as \(A\), \(B\), \(C\), \(D_1\), \(D_2\), \(D_3\), where \(D_1\), \(D_2\), \(D_3\) are the three choices.

Transformation Encoder

A traditional approach to this task would be to encode each image independently and compute the transformation as \(t = f(B) - f(A)\), following the analogy-making strategy used in models like Word2Vec. However, we found that this method was insufficient for capturing the nuanced visual relationships between images in the analogy task.

Instead, we model the transformation directly as \(t = f(A, B)\), where \(f\) is a transformer-based image encoder that leverages cross-image attention to jointly process both images. Through experiments with various vision transformer architectures (ViT and DINOv3), we determined that a ViT-based approach was the most effective for this purpose.

ViT-based Transformation Encoder Architecture

We adapt the ViT architecture, which is pretrained on 224×224 images, to process two images as a unified sequence. Here’s how:

Input Processing:

• Both input images (\(A\) and \(B\)) are independently passed through the pretrained ViT patch embedding layer
• For 224×224 images with 16×16 patches, this produces two sequences of 196 patch embeddings each, with dimension \(d\) (e.g., \(d=384\) for ViT-Small)
• These patch embeddings are concatenated and a learnable [CLS] token is prepended to form a unified sequence

Positional and Segment Embeddings:

• Positional embeddings provide spatial location information, where the embedding matrix is extended by duplicating the original patch positional embeddings for both images
• Learned segment embeddings distinguish patches from the “before” image (Segment 1) versus the “after” image (Segment 2), with Segment 0 for the [CLS] token

Transformer Processing:

• The sequence is passed through the pretrained ViT transformer blocks (12 layers for ViT-Small)
• Critically, the self-attention mechanism allows patches from image \(A\) to attend to patches from image \(B\), enabling direct comparison of corresponding spatial regions

Output:

• After layer normalization, the [CLS] token is extracted and passed through a learnable projection head consisting of linear layers, ReLU, dropout, and layer normalization
• This produces the final transformation embedding \(\mathbf{t}_{AB}^{\text{final}} \in \mathbb{R}^{e}\)

The complete forward pass can be summarized as:

\[\begin{align*} &\text{patches}_A,\, \text{patches}_B \in \mathbb{R}^{196 \times d} \\ &x = [\![\text{CLS}]\,;\, \text{patches}_A\,;\, \text{patches}_B] \in \mathbb{R}^{393 \times d} \\ &x \leftarrow x + [\text{pos}_{\text{CLS}}\,;\, \text{pos}_{\text{patches}}\,;\, \text{pos}_{\text{patches}}] \\ &x \leftarrow x + \text{SegmentEmbedding}(\text{SegmentIds}) \\ &x \leftarrow \text{TransformerBlocks}(x) \\ &\mathbf{t}_{AB}^{\text{final}} = \text{ProjectionHead}(\text{LayerNorm}(x)[0]) \in \mathbb{R}^{e} \end{align*}\]

Loss Function

After comparing the standard triplet loss and softmax cross-entropy loss, we found that a simple contrastive analogy loss performed best. Given a training example consisting of an example transformation \(\mathbf{t}_{\text{ex}}\), one correct choice transformation \(\mathbf{t}_{\text{pos}}\), and \(n\) incorrect choice transformations \(\{\mathbf{t}_{\text{neg}_i}\}_{i=1}^{n}\), the loss aims to:

• Maximize the similarity between \(\mathbf{t}_{\text{ex}}\) and \(\mathbf{t}_{\text{pos}}\)
• Minimize the similarity between \(\mathbf{t}_{\text{ex}}\) and each \(\mathbf{t}_{\text{neg}_i}\)
• Enforce a margin \(m\) between positive and negative similarities

The loss is defined as:

\[\mathcal{L} = \frac{1}{n-1}\sum_{i=1}^{n-1} \max\left(0, m - \left(s_{\text{pos}} - s_{\text{neg}_i}\right)\right)\]

where \(s_{\text{pos}} = \text{sim}(\mathbf{t}_{\text{ex}}, \mathbf{t}_{\text{pos}})\) and \(s_{\text{neg}_i} = \text{sim}(\mathbf{t}_{\text{ex}}, \mathbf{t}_{\text{neg}_i})\) are the cosine similarities. In the KiVA challenge with \(n=3\) choices per example, we have 2 negative examples.

Experiments & Results

Implementation and Hardware: The implementation uses PyTorch for modeling and Neptune for logging. We performed the experiments on a single NVIDIA L40S GPU with 40GB of memory.

Model Configuration: We use vit_small_patch16_224 as our encoder backbone, initializing its weights with pretrained checkpoints from timm. This sets a resolution of 224×224 pixels. We set the embedding dimension to \(e=512\), and the projection head consists of two linear layers with a ReLU activation, dropout, and layer normalization, mapping the ViT output to the final embedding space. This gives the model a total of 22.7M learnable parameters.

Training Configuration: The optimizer AdamW with weight decay \(1 \times 10^{-4}\) is used to train the model. A cosine annealing schedule is used to decay the learning rate over 20 total epochs, starting from \(3 \times 10^{-5}\) for the encoder parameters and \(3 \times 10^{-4}\) for the projection parameters. The batch size is 64 with a gradient accumulation of 4 for an effective batch size of 256. The contrastive margin is \(m = 0.05\). We use mixed precision training to speed up the training process.

Training Data: We use the code from the official KiVA dataset to augment the provided training data. Our pipeline generates random training samples on-the-fly that follow a similar distribution as the official training set. We include transformations with parameter combinations not present in the original training set to improve model generalization. We set the epoch length to 65,536 examples, 2,752 of which come from the official training set, and the rest are generated on-the-fly.

Results

The table below presents our model’s Top-1 accuracy on both validation and test sets, broken down by difficulty level. The results demonstrate the effectiveness of our approach, and the model’s generalization is excellent, as the gap between validation and test accuracy is minimal.

Split	KiVA (Easy)	KiVA-func (Moderate)	KiVA-comp (Difficult)	Overall
Validation	100%	100%	94%	95.4%
Test	100%	100%	95%	95.9%

The figure below provides a granular breakdown of test set performance, showing that while the model performance decreases as task complexity increases, it maintains strong performance across all transformation types. The model particularly struggles with compositionality tasks involving counting.

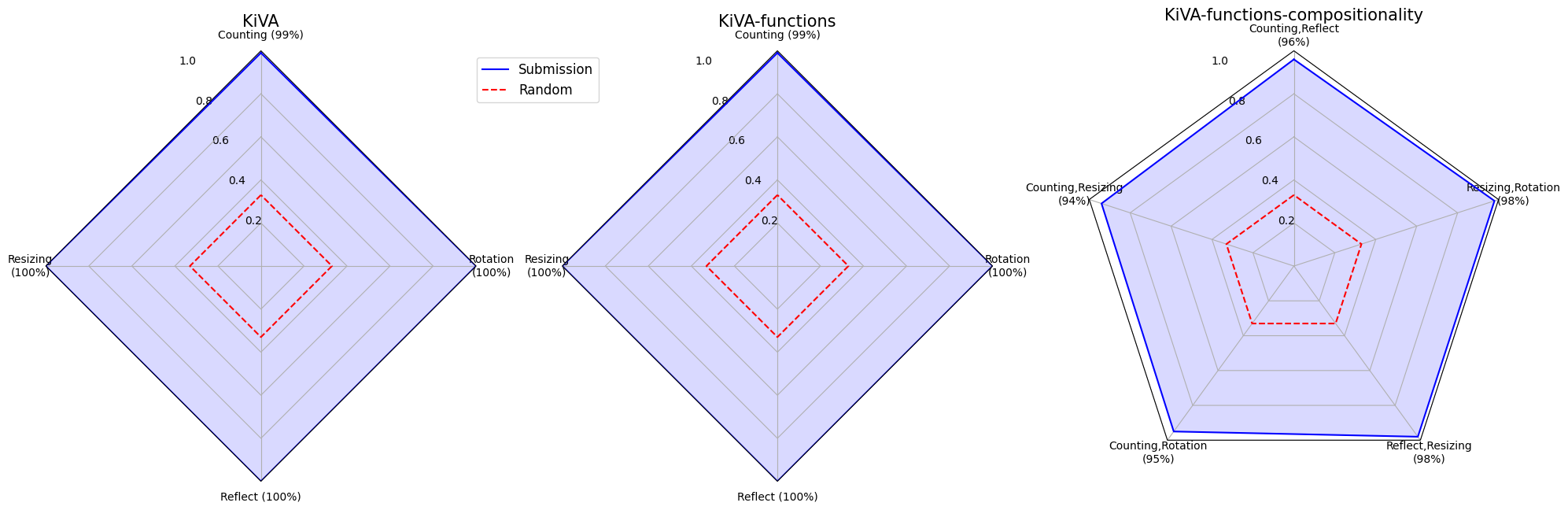
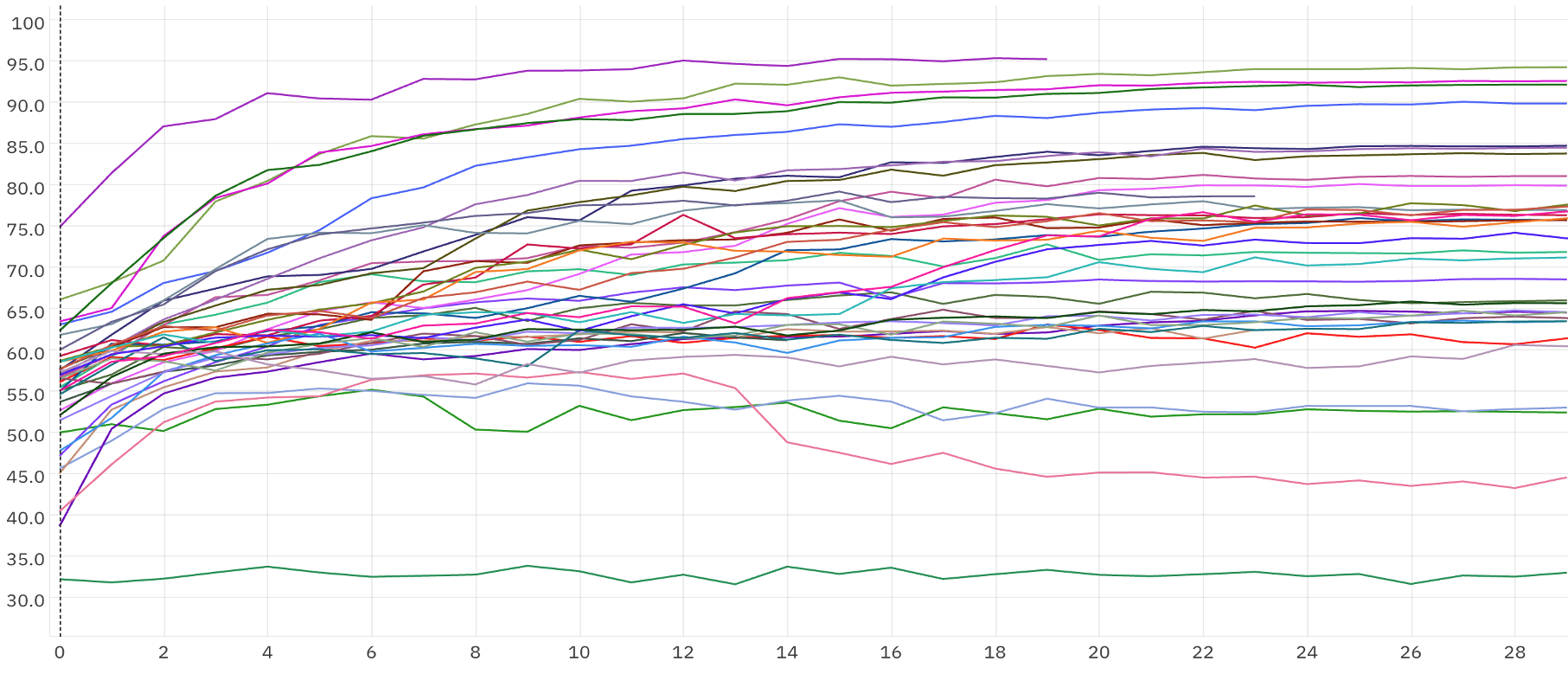
The final configuration was identified after extensive experimentation (152 runs), as illustrated by the sample of training curves below:

Conclusion

We presented a ViT-based Siamese network that processes image transformation pairs as unified sequences, enabling the direct modeling of visual changes via cross-attention. Our approach achieves 95.9% accuracy on the KiVA benchmark, demonstrating that joint encoding of transformation pairs is a highly effective strategy for visual analogical reasoning.

Key contributions include:

1. Novel architecture: Adapting ViT to process image pairs jointly rather than independently, enabling cross-image attention
2. Strong performance: Achieving near-perfect accuracy on easy and moderate difficulty levels, and 95% on the difficult compositionality tasks
3. Effective loss function: Using a simple contrastive analogy loss that outperformed more complex alternatives
4. Data augmentation: Generating additional training samples on-the-fly to improve generalization

This architecture provides a strong foundation for future work on visual reasoning tasks. The success of joint encoding suggests that cross-attention between related images is crucial for capturing subtle visual transformations that are key to analogical reasoning.

References

• Gentner, D. (1983). Structure-mapping: A theoretical framework for analogy. Cognitive Science, 7(2), 155-170.
• Yiu, E., et al. (2025). KiVA: Kid-inspired Visual Analogies for testing robust reasoning in vision-language models.
• Chicco, D. (2021). Siamese neural networks: An overview. Artificial Neural Networks, 73-94.
• Chopra, S., Hadsell, R., & LeCun, Y. (2005). Learning a similarity metric discriminatively, with application to face verification. CVPR.
• Mikolov, T., et al. (2013). Efficient estimation of word representations in vector space. ICLR.